
커패시터는 위 그림과 같이 전하를 모을 수 있는 구조로 만들어진다. 이때 양 단에 전압원을 걸면 커패시터의 양단에 전하가 모이면서 전하가 충전이 된다. 이 때 이상적인 경우는 전하를 계속 유지하지만 실제로는 자연적으로 이 전하가 조금씩 흩어져서 방전이 된다.
충전시 RC 시정수에 따라 충전의 시간이 달라지는데 이때 직렬로 연결된 저항과 커패시터의 크기에 비례한다. 아래의 τ는 RC 시정수라고 하며 단위는 초(sec)다. 즉 충전의 시간의 비례량이라고 보면 된다.

식을 보면 R과 C에 비례하는데 당연한 이야기이다. τ가 크다는것은 그만큼 충전시 시간이 많이 걸린다는 이야기이므로 R이 크면 직렬회로에서 흐르는 전류의 양이 작아지니 같은 양을 충전할 때 시간이 많이 걸릴 것이고 C가 크다는 말은 충전할 양이 많다는 이야기이므로 충전시간이 오래걸린다는 것이다.
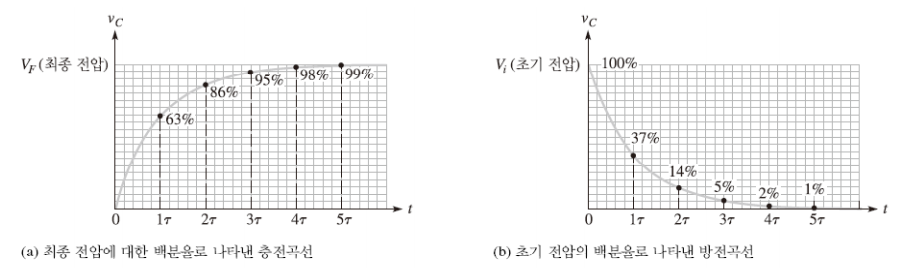
커패시터는 위 그림과 같이 비선형 곡선을 따라 충전되거나 방전된다. 보면 τ에 비례하여 시간이 정해진다. 이 곡선은 RC 회로에서는 모두 동일한 모양으로 충전된다. 뭐 간단하게 다 모르더라도 기억해야 하는 것은 바로 저 5τ이다.
5τ일 때 99% 충전이므로 만충으로 보면 된다. 즉, 어떤 커패시터를 충전하는데 걸리는 시간을 알고 싶으면 그 회로의 충전하는 전류를 결정하는 저항의 값과 충전하려는 커패시터 값을 알면 만충되는데 걸리는 시간을 알 수 있다.
중요한 것은 충전이든 방전이든 약 절반(63%) 충전하려면 RC(τ)이고 만충은 5RC(5τ)라는 정도만 알아두자.
'전자 이야기 > 전자 회로 기초' 카테고리의 다른 글
| [부품] 제너 다이오드 (Zener Diode) (0) | 2021.06.12 |
|---|---|
| [정류기] 다이오드 정류기 (0) | 2021.06.10 |
| [전자] 전압 분배 (0) | 2021.06.03 |
| [회로] 저항의 직렬, 병렬 접속 (0) | 2021.05.21 |
| [회로] 커패시터의 직,병렬 연결 (0) | 2021.05.20 |
