728x90
반응형
드모르간의 정리
(1) 이중성의 원리
부울대수의 식에서 0과 1, +와 *을 동시에 교환한 식은 반드시 성립한다는 것이다.
예를 들면 부울대수의 각 정리의 식은 다음의 5가지 조작을 행하면 된다.
① 모든 +는 *로 바꾼다.
② 모든 *는 +로 바꾼다.
③ 모든 1을 0으로 바꾼다.
④ 모든 0을 1로 바꾼다.
⑤각 논리변수는 그대로 둔다.
즉 0 + A = A에 위의 이중성의 원리를 적용시키면
1․A = A
식이 된다. 또한 A + A = A에 이중성의 원리를 적용시키면
A․A = A
식이 된다.
(2)일반화된 드모르간의 정리

이것은 논리합(OR)와 논리적(AND)이 완전히 독립되어 성립하는 것이 아니라 부정(NOT)을 조합시켜서 상호교환이 가능하도록 하는 중요한 정리로서 논리적 교합의 구성상 필수적인 성질의 것이다. 이것은 논리식의 간단화 또는 변환등에 많이 사용되는 중요한 정리이다. 드모르간의 정리는 Shannon에 의해서 아래와 같이 일반화 된다.
드모르간의 정리의 예를 들면 다음과 같다.

(3) 논리함수의 부정
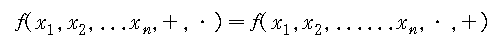
논리함수의 부정을 만들려면 어떤 논리함수에 다음과 같은 5가지 조작을 행하면 된다.
① 모든 ․을 + 로 바꾸면 된다.
② 모든 +를 ․로 바꾸면 된다.
③ 모든 1을 0로 바꾼다.
④ 모든 0을 1로 바꾼다.
⑤ 각 논리함수의 부정을 취한다.
예로서 다음 논리식 의 부정을 취해보면
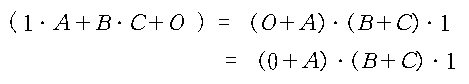
728x90
반응형
'전자 이야기' 카테고리의 다른 글
| [발진기] 발진의 조건과 Wien-Bridge Oscillator (0) | 2020.02.05 |
|---|---|
| 램에 대하여 (0) | 2020.02.05 |
| [논리게이트] AND, OR, NOT, NAND, NOR의 회로 (0) | 2020.01.28 |
| 전자정보통신 약어정리 (0) | 2020.01.17 |
| 서지(Surge)와 서지 전압(Surge Voltage) (0) | 2020.01.08 |
